Core Data and Aggregate Fetches In Swift
You can find other articles on the interwebs about NSExpression and NSExpressionDescription, however, I wasn’t really satisfied with the explanations I’ve seen. I decided to write a post myself after I recently had to become much more intimate with the way Core Data aggregate fetches work. I hope this will make clear what has to be done in order to harness this powerful feature of Core Data.
You’ve heard it said before and sometimes in a scolding tone, “CORE DATA IS NOT A DATABASE. IT’S AN OBJECT GRAPH!”. What normally follows is a discussion about what that means, if you’re lucky. Otherwise, you’re just on your own to go figure it out. In my mind, though, it’s not necessarily wrong to think of it as a database as they have enough things in common to make it a reasonable thing to do and at the end of the day Core Data is backed by a SQLite database. I think that if it helps you understand what is going on behind the scenes better, then go for it. You do have to remember some key differences that can bite you like the need to fetch before updating or deleting, for example. Though with recent additions–last year with iOS 8’s NSBatchUpdateRequest (link to iOS 8 API diff since it’s not currently documented) which allows you to perform a batch update similar to a SQL update query or this year with iOS 9’s NSBatchDeleteRequest (See WWDC 2015 session 220 for more info) which allows for batch deletes based on whatever predicate you give it, the lines seem to be blurring more and more.
tl;dr; Get the source code here: Core Data and Aggregate Fetches Code on Github. The project and source were created with Xcode 7 beta and Swift 2.0 but they’ve now been updated to Xcode 8 and Swift 3.
When it comes to aggregating data, or in more simple database-y terms, data you want to group by, it’s not immediately obvious in Core Data how to go about what you need using a fetch–to the point where some have wondered if it was even possible. It would be nice if there were some mechanism or even syntactic sugar around it that would make it a little more database-y since that makes it easier to grasp, but I think that if we start from a database SQL query and work our way back to a Core Data fetch that uses NSExpression and NSExpressionDescription, it will make a whole lot more sense. Let’s get started by considering some data:
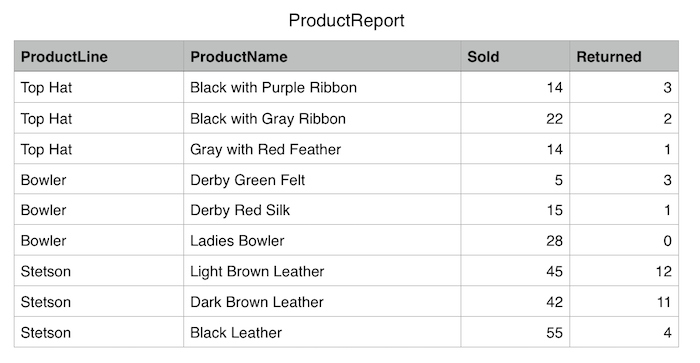
I’ve seen this kind of data many times. It’s a report that you might get from a company who wants to display sales reports for reps or customers. You can see that this data is flattened. It’s not normalized. Instead of using multiple tables you have a single table that has a way to represent a parent entity. In the case of the data above, this is represented by the column called “ProductLine”. In SQL, if we wanted to get a report of the total sum of all of the items grouped by product line, it would go something like this:
SELECT ProductLine, SUM(Sold) as SoldCount FROM Products GROUP BY ProductLine
And the results would looks something like this:
ProductLine SoldCount ----------- ---------- Bowler 48 Stetson 142 Top Hat 50
So the question is, how do we translate this query into a Core Data fetch?
The Basics of Aggregate Fetching
The concept behind the SQL query is simple and easy to understand, but until you see how each component part of the query translates to a Core Data NSExpression or NSExpressionDescription it can be a little confusing getting the results you want in Core Data. Here are a few basic points that will clarify things a little as we head into writing our Core Data query code.
- When you fetch the records, you are going to be requesting that Core Data returns you an array of dictionaries. This makes sense if you think about it. You won’t get back a list of managed objects because the data doesn’t represent a single record and therefore entity. Instead, it represents rows in your data model that have been manipulated to provide an aggregate dataset–a sum of all rows grouped by product line in our case.
- Just as in the SQL query, you need a name for your aggregate “column”. When you run the query directly in SQLite, you don’t have to use the “as” keyword and provide a label–it will provide one for you. However, in your Core Data Query, you’re going to need to name your aggregate column.
- Just as in the SQL query, you need to list the columns you want to group by. This will be the same column names you listed in your select minus the aggregate columns.
Our final aggregate query that we’re going to build is going to also include a sum of the returned counts. It looks like this:
SELECT ProductLine, SUM(Sold) as SoldCount, SUM(Returned) as ReturnedCount FROM Products GROUP BY ProductLine
And the output of this query using the SQLite CLI looks like this:
ProductLine SoldCount ReturnedCount ----------- ---------- ------------- Bowler 48 4 Stetson 142 27 Top Hat 50 6
Fetching Some Aggregate Data
When a fetch request is handed to your managed object context to fetch your data it needs to have a list of columns you want to use for your fetch specified by a list of either NSExpressionDescription objects or Strings. Here’s how to determine which one you should use. Look again at our query:
SELECT ProductLine, SUM(Sold) as SoldCount, SUM(Returned) as ReturnedCount FROM Products GROUP BY ProductLine
We have three items we want returned. “ProductLine” is an actual column in our table–for that we should use a String, while SoldCount and ReturnedCount are new columns we are creating for our query result. They need to be added as NSExpressionDescription objects.
NOTE: The data we’ve been using in the discussion up until now is contrived other than having been placed into a Numbers spreadsheet and, from there (as CSV), imported into a SQLite database just to run the command line queries–the results of which you’ve seen above. Here, however, we depart from that data and will reference similar fields, but ones that we are actually using in the demo project. The differences are subtle, “ProductLine” vs “productLine”, etc. however, it seems important to mention since the following will seem inconsistent unless we explain. Carry on.
If you look at the signature for the property propertiesToFetch on NSFetchRequest you see it takes an array of Any:
@available(iOS 3.0, *)
open var propertiesToFetch: [Any]?
So when your fetch request is ready to execute, you just give it an array containing Strings and NSExpressionDescriptions. Here is how I begin my code to build up these expressions.
var expressionDescriptions = [AnyObject]()
expressionDescriptions.append("productLine" as AnyObject)
As a first step I go ahead and append the Strings I need as you can see above. Next, I go ahead and build up the expression description objects. Let’s take the first one, SoldCount, and see how it is setup in code:
// Create an expression description for our SoldCount column
var expressionDescription = NSExpressionDescription()
// Name the column
expressionDescription.name = "SoldCount"
// Use an expression to specify what aggregate action we want to take and
// on which column. In this case sum on the sold column
expressionDescription.expression = NSExpression(format: "@sum.sold")
// Specify the return type we expect
expressionDescription.expressionResultType = .integer32AttributeType
Now that it this one is built out, add it to our AnyObject array:
// Append the description to our array
expressionDescriptions.append(expressionDescription)
Now let’s do the same for our ReturnedCount column:
// Create an expression description for our ReturnedCount column
expressionDescription = NSExpressionDescription()
// Name the column
expressionDescription.name = "ReturnedCount"
// Use an expression to specify what aggregate action we want to take and
// on which column. In this case sum on the returned column
expressionDescription.expression = NSExpression(format: "@sum.returned")
// Specify the return type we expect
expressionDescription.expressionResultType = .integer32AttributeType
And add it to the array as well:
// Append the description to our array
expressionDescriptions.append(expressionDescription)
All that’s left now is to build up our fetch request.
Put It All Together
When we create our fetch request the two fields that are most pertinent are the propertiesToGroupBy, and propertiesToFetch. In the propertiesToGroupBy we provide an array containing just the one field, “productLine”. In the propertiesToFetch we specify our AnyObject array that contains Strings and NSExpressionDescription objects. Here is the code to build up the fetch request.
// Build out our fetch request the usual way
let request = NSFetchRequest(entityName: self.entityName)
// This is the column we are grouping by. Notice this is the only non aggregate column.
request.propertiesToGroupBy = ["productLine"]
// Specify we want dictionaries to be returned
request.resultType = .dictionaryResultType
// Hand off our expression descriptions to the propertiesToFetch field. Expressed as strings
// these are ["productLine", "SoldCount", "ReturnedCount"] where productLine is the value
// we are grouping by.
request.propertiesToFetch = expressionDescriptions
You can set other fields on the fetch request as usual, like adding an array of NSSortDescriptors, for example:
// Go ahead and specify a sorter
request.sortDescriptors = [NSSortDescriptor(key: "productLine", ascending: true)]
Finally, here is what the code looks like altogether as a class function on our NSManagedObject subclass:
class func aggregateProductsInContext(context:NSManagedObjectContext) -> [[String:AnyObject]]? {
// Create an array of AnyObject since it needs to contain multiple types--strings and
// NSExpressionDescriptions
var expressionDescriptions = [AnyObject]()
// We want productLine to be one of the columns returned, so just add it as a string
expressionDescriptions.append("productLine" as AnyObject)
// Create an expression description for our SoldCount column
var expressionDescription = NSExpressionDescription()
// Name the column
expressionDescription.name = "SoldCount"
// Use an expression to specify what aggregate action we want to take and
// on which column. In this case sum on the sold column
expressionDescription.expression = NSExpression(format: "@sum.sold")
// Specify the return type we expect
expressionDescription.expressionResultType = .integer32AttributeType
// Append the description to our array
expressionDescriptions.append(expressionDescription)
// Create an expression description for our ReturnedCount column
expressionDescription = NSExpressionDescription()
// Name the column
expressionDescription.name = "ReturnedCount"
// Use an expression to specify what aggregate action we want to take and
// on which column. In this case sum on the returned column
expressionDescription.expression = NSExpression(format: "@sum.returned")
// Specify the return type we expect
expressionDescription.expressionResultType = .integer32AttributeType
// Append the description to our array
expressionDescriptions.append(expressionDescription)
// Build out our fetch request the usual way
let request = NSFetchRequest(entityName: self.entityName)
// This is the column we are grouping by. Notice this is the only non aggregate column.
request.propertiesToGroupBy = ["productLine"]
// Specify we want dictionaries to be returned
request.resultType = .dictionaryResultType
// Go ahead and specify a sorter
request.sortDescriptors = [NSSortDescriptor(key: "productLine", ascending: true)]
// Hand off our expression descriptions to the propertiesToFetch field. Expressed as strings
// these are ["productLine", "SoldCount", "ReturnedCount"] where productLine is the value
// we are grouping by.
request.propertiesToFetch = expressionDescriptions
// Our result is going to be an array of dictionaries.
var results:[[String:AnyObject]]?
// Perform the fetch. This is using Swfit 2, so we need a do/try/catch
do {
results = try context.fetch(request) as? [[String:AnyObject]]
} catch _ {
// If it fails, ensure the array is nil
results = nil
}
return results
}
When this function returns, we get a nice tidy little array of dictionaries that looks something like this:
[
["SoldCount": 48, "productLine": Bowler, "ReturnedCount": 4],
["SoldCount": 142, "productLine": Stetson, "ReturnedCount": 27],
["SoldCount": 50, "productLine": Top Hat, "ReturnedCount": 6]
]
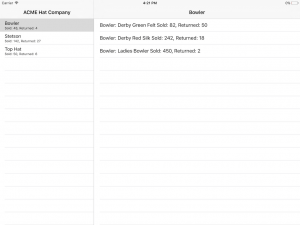
Which is exactly what we want. We can then just use this array directly as our data for our UITableView data source on the master side of our split view controller. Here is what our app looks like with the data fully populated (click to enlarge):
You can see that we’ve built out the detail side of the split view controller to also display a table view that contains a list of all of the products for the selected product line. Take a look at the source project on GitHub and build the source yourself to see how it all comes together. This post and the source code for it have now been updated to Swift 3 and Xcode 8.
Conclusion
For me the impetus of mastering the aggregate fetch was poor performance doing it another way. Yes, you can achieve the results you want by performing aggregate functions on arrays of data manually, but I noticed in places where I was doing this in an app I work on the performance was growing steadily worse the more data the customer added to the table in question. Experience with RDBMSs (in some other lifetime) reminded me that performing the right query could be far more efficient and so the search was on to find an appropriate optimization. In the mean time I had resorted to doing a background fetch (on a background context) and calculation that loaded an activity spinner to let the user know that the fetch/calculation was occurring, but I hated doing that to my users–and I guarantee they hated that experience. Once I found a way to properly do an aggregate fetch (as demonstrated in this post), I didn’t even have to perform it in the background. What was taking up to 30 seconds before, was now taking milliseconds. That is a nice optimization that makes for happier users. Until next time.